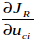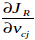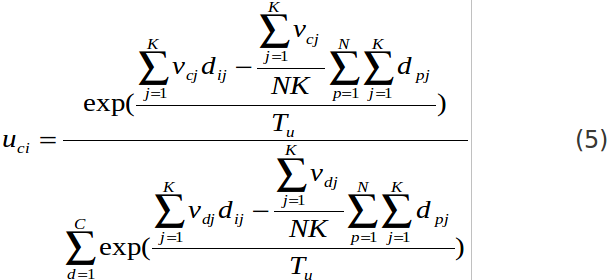A partitioning based algothim to fuzzy co-cluster documents and words =
這篇文章主要是看完作者Wiliam-Chandra Thjhi,Lihui Chen 所寫下的心得
introduction ==
在資料檢索中,文件的分類是個很重要的過程.他的應用包括新一代Web,目錄,查詢的擴展,視覺化的收尋.
儘管他是重要的但檢索文件尚未達到充分的發揮.有些問題仍然存在著,例如在練習過程的精確度,缺乏的分群解釋,
對於雜訊很敏感.而目前許多優越的計算以發展來對付這些問題.
處理低的精確度是由於高的維度,數個子空間的分群演算法,包括各種維度簡化的技術像是矩陣的分解,特徵分類或雙分群,
和項目的修剪的技術已在(F;orian et al.,2002)介紹過了.彈性的分類演算法已提出而穫得不確定的邊界條件.因此
改善去描述分類的解釋.一些重要的方法如fuzzy(Friedman et al,2004)和粗略集合(Lingras and West,2004;
Lingras er al,2004)的分類演算法,這兩篇論文而分類是分別表示為fuzzy集合與粗略的集合.特徵值選取技術已可以
去除資料的雜訊.有些進階文件的分群技術包括神經網路分群,機率,分佈分群,和片語基礎分群.在這篇文章,我們有興趣是
一個特別的模糊雙分群.
藉著執行雙分群,文件與文字是同時分類成數個分群.每一個雙分群是由一對高度相關文件(document)分群與文字(word)
分群所構成.雙分群提供一些如維度的減少,文件分群的解釋,和精準度的改善.Fuzzy雙分群更進一步使用屬性函數改善分群的重疊
,這些優越使得Fuzzy分群適合分類文件,特別運用在網際網路上.
數個fuzzy雙分群的演算法已先前出版(Frigui and Nasaoui,2004;Kummamuru et al.,2003;Oh et al.,2001)
他們產生Fuzzy雙分群藉著他們各別的物件函數.儘管有不同目標函數,這三個演算法都有共同的約束條件,因為這些約束條件僅只能
反映出文字屬性的加權而沒有描述出natrual fuzzy.再資料檢索有些實際的價值,例如:變寬的搜尋,引擎的查詢,依次可能改善的
特性,所以要發展出一個新的技術
這篇文章提出新的fuzzy分群技術,產生文件與文字的分類演算法,這邊稱為FCR,主要是在文件與文字附加上Ruspini`s conditoin,
而在FCR中的物件函數事由(oh et al 2001)提出,因而修改才能獲得natural fuzzy word cluster.
Fuzzy co-cluster with Ruspini`s condition
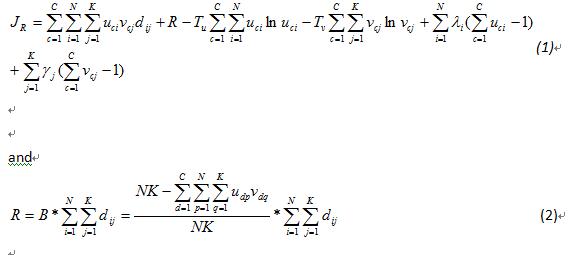
以上的係數我們會陸陸續續作介紹
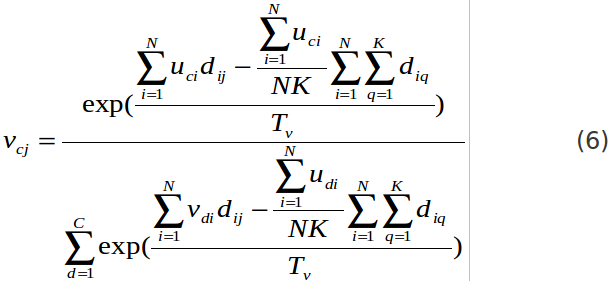
C:分群個數,N:文件個數,K:文字個數
uci:i在c中的屬性,vcj:j在c中的屬性,
dij:加權函數(類似正規化)
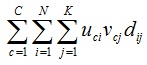 把這項稱之為聚集度(由oh et al 2001所稱呼),dij這個項目是與document i and word j有相互關係
把這項稱之為聚集度(由oh et al 2001所稱呼),dij這個項目是與document i and word j有相互關係
主要我們是想要文件與文字進入相同的雙分群(co-cluster),而這邊告訴我們當dij值高而uci and vcj有會有高值
在這邊最大的聚合度有兩個相依的限制
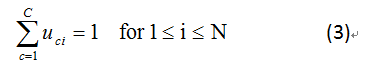
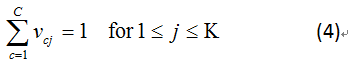
(3)式子中全部文件的屬性在co-cluster中等於1(4)式子中全部的文字的屬性在co-cluster中等於1,經過這兩個限制條件後,可以保證產生fuzzy
document and word clustersR這一項主要是避免產生一個fuzzy co-cluster構成全部的documents and words,至於R項後面會有更詳細的說明
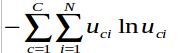 and
and 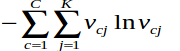 分別是document和words的模糊化器,而Oh et al(2001)也使用相同的模糊化器,這裡的模糊化器有
分別是document和words的模糊化器,而Oh et al(2001)也使用相同的模糊化器,這裡的模糊化器有
兩個目的,第一個主要是正規化.第二個主要是使document和words模糊化
接下來我們討論R項
當我們把全部的documents and words 加上Ruspini`s condition 來避免在全部的documents and words落在one co-cluster,以下會詳盡介紹這個R
,首先我們先沒有考慮這個R項如以下公式
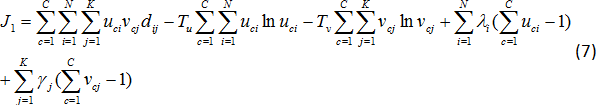
考慮U and V為 document membership and word membership matrices如下
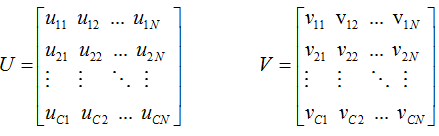
定義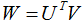 ,上標的T為轉置符號
,上標的T為轉置符號
,然而W矩陣如下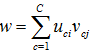 (8),D表示為document-word weight matrix
(8),D表示為document-word weight matrix
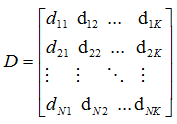 (9),注意W和D有相同的列跟行,他可以表示出degree of aggregation(聚合度)公式如下
(9),注意W和D有相同的列跟行,他可以表示出degree of aggregation(聚合度)公式如下
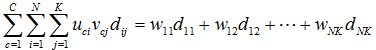 (10),當(7)是當成物件函數時,其中在W中的各個
(10),當(7)是當成物件函數時,其中在W中的各個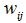 元素都會小於或等於1,在這裡我們考慮兩個membership vectors
元素都會小於或等於1,在這裡我們考慮兩個membership vectors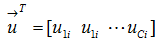 and
and 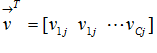 .基於(8)式子我們得知
.基於(8)式子我們得知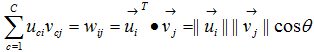 ,其中
,其中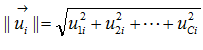
由於Ruspini`s condition 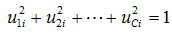 所以可以得知
所以可以得知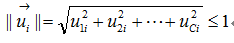 ,同樣的
,同樣的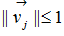 and
and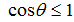 .因此
.因此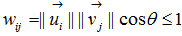 這邊我們考慮W為單位矩陣,例如全部的元素都為1,由式子(10)我們可以計算出 degree of aggregation為
這邊我們考慮W為單位矩陣,例如全部的元素都為1,由式子(10)我們可以計算出 degree of aggregation為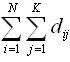 ,如果
,如果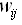 小於1br]的時候degree of aggregation小於[[Image(dsum.jpg)?,所以當W為單位矩陣時,在(7)式子中的
小於1br]的時候degree of aggregation小於[[Image(dsum.jpg)?,所以當W為單位矩陣時,在(7)式子中的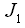 有global maxmum
有global maxmum
Attachments (30)
-
cocluster公式.jpg
(16.6 KB) -
added by adherelinux 15 years ago.
cocluster公式
-
aggregation.jpg
(5.5 KB) -
added by adherelinux 15 years ago.
aggregation
-
uci.jpg
(1.8 KB) -
added by adherelinux 15 years ago.
uci
-
vcj.jpg
(1.9 KB) -
added by adherelinux 15 years ago.
vcj
-
lnu.jpg
(2.6 KB) -
added by adherelinux 15 years ago.
lnu
-
lnv.jpg
(2.5 KB) -
added by adherelinux 15 years ago.
lnv
-
du.jpg
(23.3 KB) -
added by adherelinux 15 years ago.
du
-
dv.jpg
(23.4 KB) -
added by adherelinux 15 years ago.
dv
-
djdu.jpg
(1.1 KB) -
added by adherelinux 15 years ago.
djdu
-
djdv.jpg
(1.1 KB) -
added by adherelinux 15 years ago.
djdv
-
J1.jpg
(4.6 KB) -
added by adherelinux 15 years ago.
J1
-
UV.jpg
(3.8 KB) -
added by adherelinux 15 years ago.
U V
-
W.jpg
(654 bytes) -
added by adherelinux 15 years ago.
W
-
Wmatrix.jpg
(2.3 KB) -
added by adherelinux 15 years ago.
Wmatrix
-
wij.jpg
(991 bytes) -
added by adherelinux 15 years ago.
wij
-
D.jpg
(2.1 KB) -
added by adherelinux 15 years ago.
D
-
sumuvd.jpg
(1.9 KB) -
added by adherelinux 15 years ago.
sumuvd
-
w.jpg
(389 bytes) -
added by adherelinux 15 years ago.
w
-
uT.jpg
(911 bytes) -
added by adherelinux 15 years ago.
UT
-
VT.jpg
(955 bytes) -
added by adherelinux 15 years ago.
VT
-
sumuv.jpg
(2.0 KB) -
added by adherelinux 15 years ago.
sumuv
-
|UT|.jpg
(1.1 KB) -
added by adherelinux 15 years ago.
|UT|
-
sumu=1.jpg
(846 bytes) -
added by adherelinux 15 years ago.
sumu
-
U<=1.jpg
(1.2 KB) -
added by adherelinux 15 years ago.
U<=1
-
v<=1.jpg
(608 bytes) -
added by adherelinux 15 years ago.
V<=1
-
cos.jpg
(543 bytes) -
added by adherelinux 15 years ago.
cos<=1
-
wij<=1.jpg
(1.3 KB) -
added by adherelinux 15 years ago.
wij<=1
-
dsum.jpg
(932 bytes) -
added by adherelinux 15 years ago.
dsum
-
w_ij.jpg
(372 bytes) -
added by adherelinux 15 years ago.
wij
-
J_1.jpg
(347 bytes) -
added by adherelinux 15 years ago.
J1
Download all attachments as: .zip